Сторона треугольника и формула онлайн

Типы треугольников

По величине углов

1. Остроугольный треугольник — все углы треугольника острые.

   Читайте также: Где найти Сороку в Сталкер Зов Припяти

2. Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).

3. Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).

По числу равных сторон

1. Разносторонний треугольник — все три стороны не равны.

   Читайте также: Конспект по математике "Десятичная дробь"

2. Равнобедренный треугольник — две стороны равны.

3. Равносторонним треугольник или правильный треугольник — все три стороны равны.

Видео

Стороны в прямоугольном треугольнике

В прямоугольном треугольнике (рис. 2) стороны и , образующие прямой угол, называются катетами, а третья сторона – гипотенузой. Связаны стороны прямоугольного треугольника теоремой Пифагора: «Квадрат гипотенузы равен сумме квадратов катетов»

Решение треугольника по двум сторонам и углу между ними

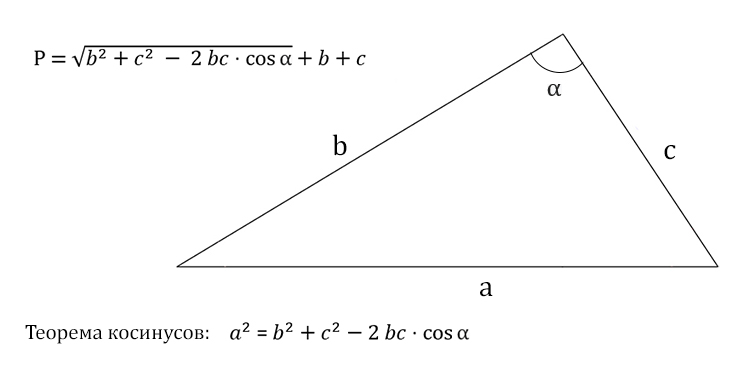
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Решение:

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

найдем cosA:

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Вычисления выше легко производить инженерным онлайн калькулятором.

Из формулы (3) найдем cosA:

Используя онлайн калькулятор для arcsin и arccos или инженерный онлайн калькулятор находим угол A:

.

Поскольку уже нам известны два угла то находим третий:

.

Подобие треугольников

Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.

∆АВС ~ ∆MNK => α = α₁, β = β₁, γ = γ₁ и ABMN = BCNK = ACMK = k,

где k — коэффициент подобия Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:

S_∆АВСS_∆MNK = k²

Теги