Теорема о величине внешнего угла треугольника по геометрии 7 класса

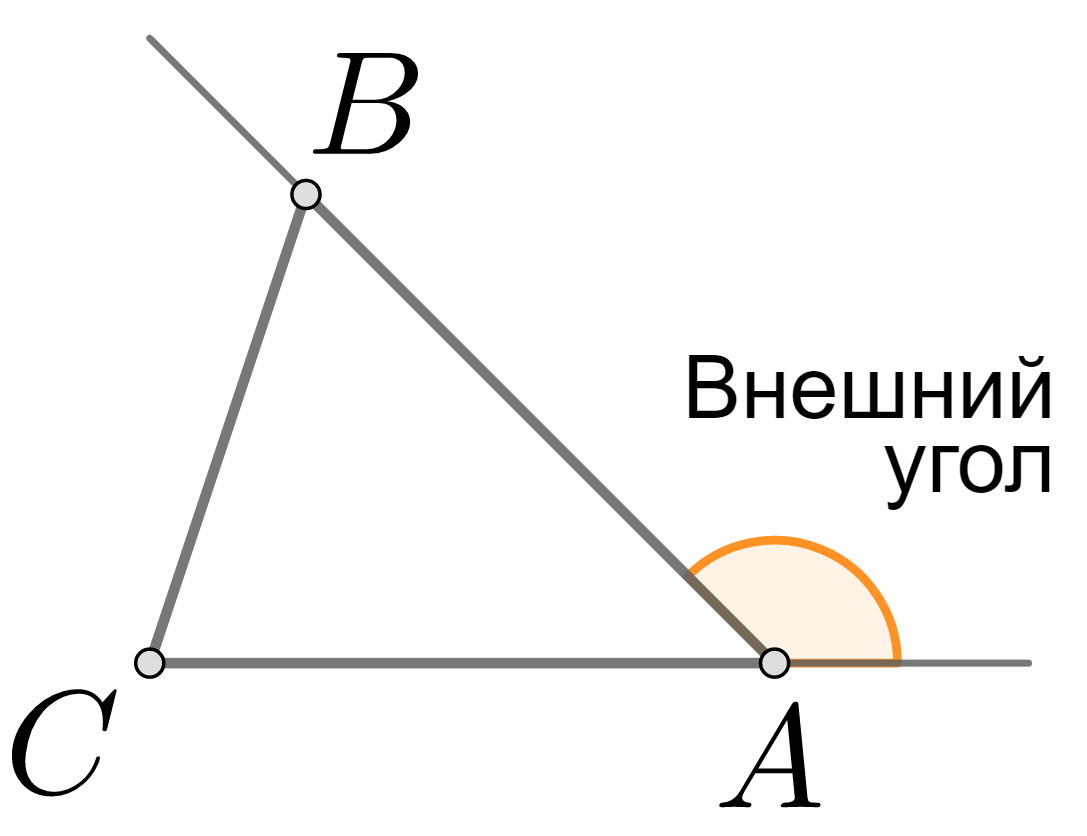
Свойства внешнего угла

1. Внешний угол треугольника равен сумме внутренних углов не смежных с ним:

     

   Читайте также: Как вычислить общее сопротивление цепи
2. Сумма внешнего и внутреннего углов при одной вершине равна :

     

3. Сумма внешних углов треугольник взятых по одному при каждой вершине равна .
4. Внешние углы при одной вершине треугольника равны между собой (как вертикальные):

     

Видео

Диагонали n угольника

Число диагоналей n – угольника равно

Фигура	Рисунок	Описание
Диагональмногоугольника		Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника
Диагонали n – угольника, выходящие из одной вершины		Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника
Все диагонали n – угольника

Диагональ многоугольника

Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника

Диагонали n – угольника, выходящие из одной вершины

Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника

Все диагонали n – угольника

Число диагоналей n – угольника равно

Внешний угол многоугольника

      Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).

Рис.1

      Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).

Рис.2

      Замечание. Мы рассматриваем только выпуклые многоугольникивыпуклые многоугольники.

Чему равен, как найти при вершине

Определение

Для того, чтобы найти ВУТ при вершине, необходимо сложить значения не соседних с ним частей плоскости, которые ограничены двумя лучами, рассматриваемой геометрической фигуры.

Продемонстрируем это положение на примерах.

Задача №1

В треугольнике DEF угол D = 50^°, а F = 45^°. Найти: ВУ при каждой вершине фигуры.

Решение

Сумма углов треугольника всегда равна 180°. Из этого следует, что \angle E=180˚-\angle D-\angle F=85^\circ. ВУ при точке соединения сторон DE и DF будет равняться сложенным внутренним углам при вершинах E и F, а это 130°. Соответственно, ВУ при E составляет 95°, а при F — 135°.

Ответ: ∠ D = 130°, ∠  E = 95°, ∠ F = 135°. 

Задача №2

В треугольнике ABC ВУ при вершине A = 68°, а при вершине C = 55°. Найти: Внутренний угол при B. На иллюстрации отображены пронумерованные названия углов.

Решение

Если сложить смежные углы, то в любом случае получится 180°. Из этого составляем равенства: ∠ A = 180° – ∠ 3 = ∠ 180° – 112° = 68°; ∠ С = 180° – ∠ 2 = ∠ 180° – 125° = 55°. Далее из сложенного вычитаем уже известное: ∠ A = 180° – ∠ A – ∠ C = ∠ 180° – 68° – 55° = 57°.

Ответ: ∠ B = 57°.

Формулировка теоремы

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

γ = α + β

Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.

Свойства углов правильного n –угольника

Фигура	Рисунок	Формулировка теоремы
Углы правильногоn – угольника		Все углы правильного n – угольника равны
Внешние углыправильногоn – угольника		Все внешние углы правильногоn – угольника равны

Углы правильного n – угольника

Все углы правильного n – угольника равны

Внешние углы правильного n – угольника

Все внешние углы правильногоn – угольника равны

Теги